The board consists of a four-by-four array of squares, each of which contains a four-by-four array of spaces. But how are these spaces connected to each other? It's really quite simple! Here's how:
- Any given space is connected to any immediately adjacent space that is in the same square.
- Any given space is also connected to its analogous space in any adjacent square.
Examples
Take a look below. The "moving from" (circled) space is connected to all the "moving to" (starred) spaces:
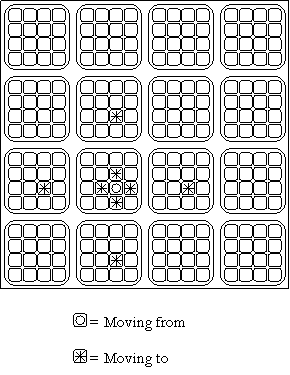
Here's another example. In this case, there is one fewer connected space available. This is because the circled space is on the edge of a square:
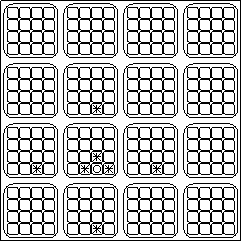
(Also notice that a space on the edge of a square is not connected to the near space on the adjacent square.)
In the following case, there are even fewer connecting spaces available. This is because the circled space resides in a corner square: