Although it is not required for playing the game, an understanding of the underlying geometry of the playing field can provide a strategic advantage.
The tesseract
In order to generate sufficient connectivity between spaces, the entire playing area was modeled after a four-dimensional structure known as a "tesseract" (also known as a "hypercube").
Although four dimensions can seem daunting, the following is a straightforward way to conceptualize the geometry:
- Start with a single point. This is a zero-dimensional object - when you're on the point, you can't go anywhere else.

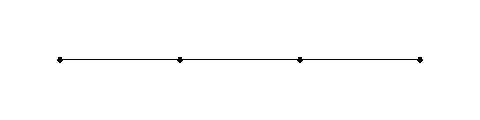
- Now multiply the point, and stretch the points apart, connecting them with a line. This is one-dimensional, because you can only go back and forth along the single line.
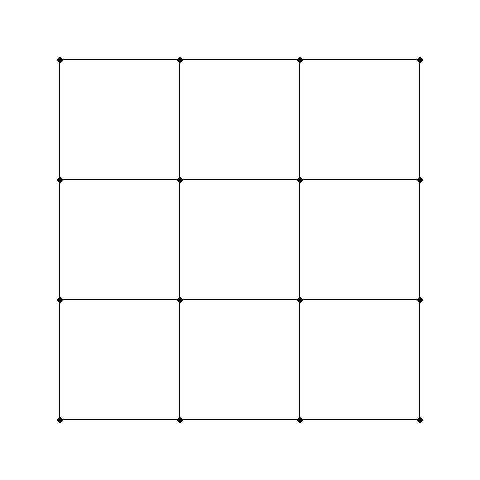
- Now multiply the line, connecting the points with additional lines. You end up with a square. This is two-dimensional because you can either go side-to-side, or up-and-down.
- Now multiply the square, and connect the dots. You have a cube, which is three-dimensional.
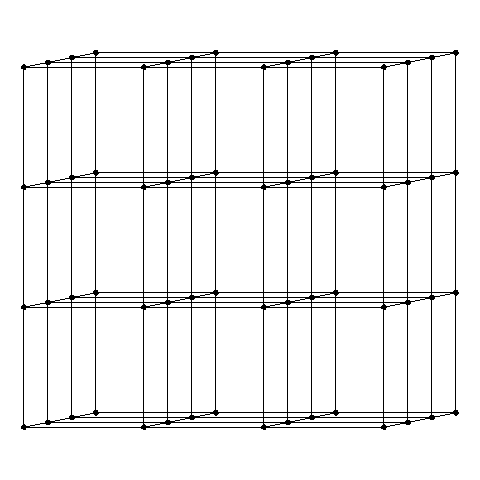
- Now multiply the cube! (This part gets tricky to visualize.) What you have is called a "tesseract" ("tesser-" means "four", and "-act" means "axis"), and it is a four-dimensional object - from any given point, you can travel along four different lines.
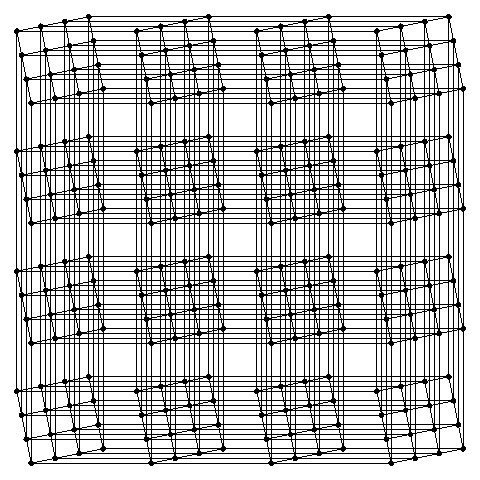
Slice it up
Now, for a playable game, we need to represent this four dimensional object in the real world. The way to do this is with slicing:
- First, we slice the tesseract into cubes.
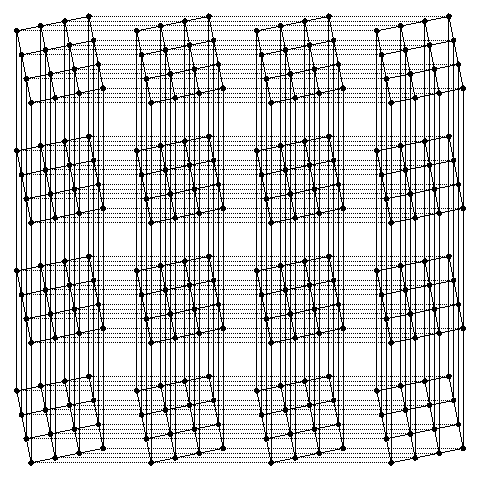
- Then, we slice the cubes into squares.
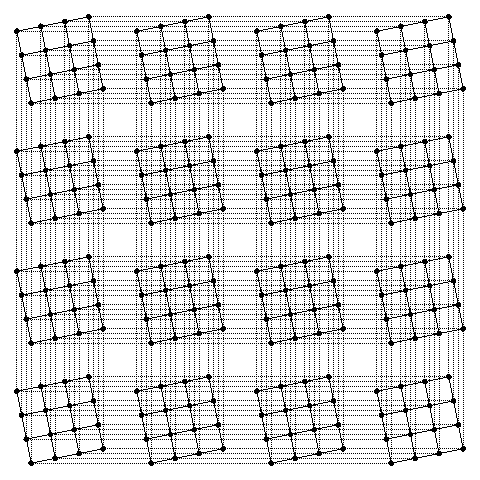
- Finally, we lay the squares out flat on the board. What results is a "square of squares", with analogous points on the squares invisibly linked.
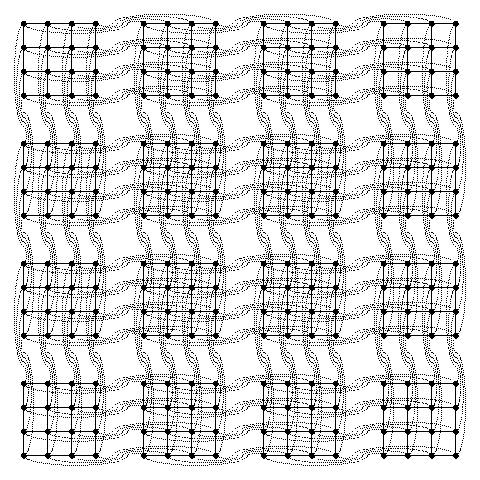
That's all there is to it!